Inverse of a Matrix
using Minors, Cofactors and Adjugate

(Note: also check out Matrix Inverse by Row Operations and the Matrix Calculator.)

We can calculate the Inverse of a Matrix by:

  • Step 1: calculating the Matrix of Minors,
  • Step 2: then turn that into the Matrix of Cofactors,
  • Step 3: then the Adjugate, and
  • Step 4: multiply that by 1/Determinant.

But it is best explained by working through an example!

Example: find the Inverse of A:

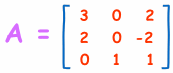
matrix A

It needs 4 steps. It is all simple arithmetic but there is a lot of it, so try not to make a mistake!

Step 1: Matrix of Minors

The first step is to create a "Matrix of Minors". This step has the most calculations.

For each element of the matrix:

  • ignore the values on the current row and column
  • calculate the determinant of the remaining values

Put those determinants into a matrix (the "Matrix of Minors")

Determinant

For a 2×2 matrix (2 rows and 2 columns) the determinant is easy: ad-bc

Think of a cross:

  • Blue means positive (+ad),
  • Red means negative (-bc)
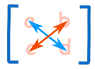 A Matrix

(It gets harder for a 3×3 matrix, etc)

The Calculations

Here are the first two, and last two, calculations of the "Matrix of Minors" (notice how I ignore the values in the current row and columns, and calculate the determinant using the remaining values):

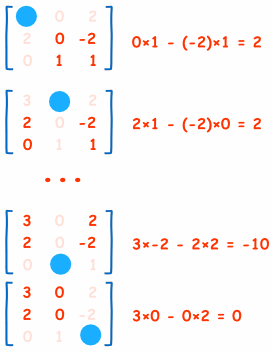
matrix of minors calculation steps

And here is the calculation for the whole matrix:

matrix minors result

Step 2: Matrix of Cofactors

checkerboard of plus and minus

This is easy! Just apply a "checkerboard" of minuses to the "Matrix of Minors". In other words, we need to change the sign of alternate cells, like this:

matrix of cofactors

Step 3: Adjugate (also called Adjoint)

Now "Transpose" all elements of the previous matrix... in other words swap their positions over the diagonal (the diagonal stays the same):

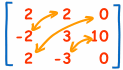
matrix adjugate

Step 4: Multiply by 1/Determinant

Now find the determinant of the original matrix. This isn't too hard, because we already calculated the determinants of the smaller parts when we did "Matrix of Minors".

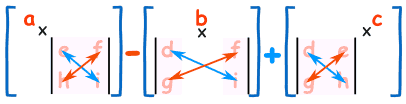
A Matrix

In practice we can just multiply each of the top row elements by the cofactor for the same location:

Elements of top row: 3, 0, 2
Cofactors for top row: 2, −2, 2

Determinant = 3×2 + 0×(−2) + 2×2 = 10

(Just for fun: try this for any other row or column, they should also get 10.)

And now multiply the Adjugate by 1/Determinant:

matrix adjugate by 1/det gives inverse

And we are done!

Compare this answer with the one we got on Inverse of a Matrix using Elementary Row Operations. Is it the same? Which method do you prefer?

Larger Matrices

It is exactly the same steps for larger matrices (such as a 4×4, 5×5, etc), but wow! there is a lot of calculation involved.

For a 4×4 Matrix we have to calculate 16 3×3 determinants. So it is often easier to use computers (such as the Matrix Calculator.)

Conclusion

  • For each element, calculate the determinant of the values not on the row or column, to make the Matrix of Minors
  • Apply a checkerboard of minuses to make the Matrix of Cofactors
  • Transpose to make the Adjugate
  • Multiply by 1/Determinant to make the Inverse